Contenuti
In questa pubblicazione considereremo cos'è una combinazione lineare di stringhe, stringhe linearmente dipendenti e indipendenti. Forniremo anche esempi per una migliore comprensione del materiale teorico.
Definizione di una combinazione lineare di stringhe
Combinazione lineare (LK) termine s1Con 2, …, Sn matrice A chiamata espressione della forma seguente:
αs1 +αs2 +…+αsn
Se tutti i coefficienti αi sono uguali a zero, quindi LC è banale. In altre parole, la banale combinazione lineare è uguale alla riga zero.
Per esempio: 0·s1 + 0 · s2 + 0 · s3
Di conseguenza, se almeno uno dei coefficienti αi non è uguale a zero, allora LC lo è non banale.
Per esempio: 0·s1 + 2 · s2 + 0 · s3
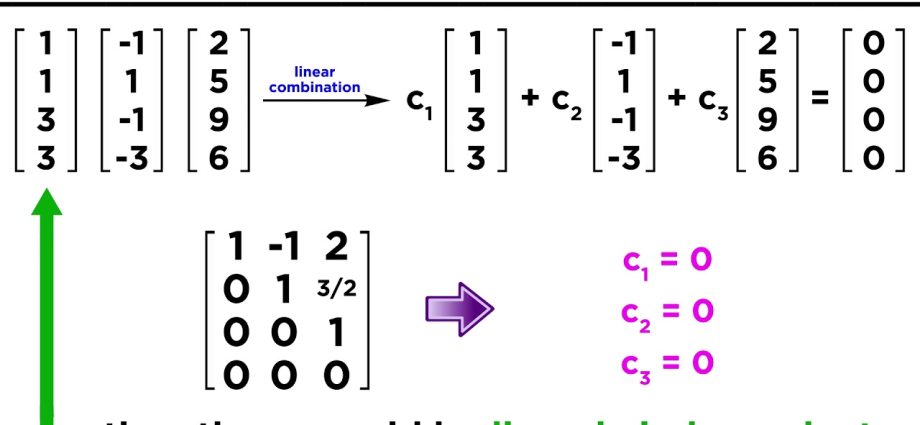
Righe linearmente dipendenti e indipendenti
Il sistema di stringhe è linearmente dipendente (LZ) se esiste una loro combinazione lineare non banale, che è uguale alla linea zero.
Ne consegue che un LC non banale può in alcuni casi essere uguale alla stringa zero.
Il sistema di stringhe è linearmente indipendente (LNZ) se solo il banale LC è uguale alla stringa nulla.
Note:
- In una matrice quadrata, il sistema di righe è un LZ solo se il determinante di questa matrice è zero (, il = 0).
- In una matrice quadrata, il sistema di righe è un LIS solo se il determinante di questa matrice non è uguale a zero (, il ≠ 0).
Esempio di un problema
Scopriamo se il sistema di stringhe lo è
Decisione:
1. Per prima cosa, creiamo un LC.
α1{3 4} + a2{9 12}.
2. Ora scopriamo quali valori dovrebbero assumere α1 и α2in modo che la combinazione lineare sia uguale alla stringa nulla.
α1{3 4} + a2{9 12} = {0 0}.
3. Facciamo un sistema di equazioni:
![]()
4. Dividi la prima equazione per tre, la seconda per quattro:
![]()
5. La soluzione di questo sistema è qualsiasi α1 и α2, Con α1 = -3a2.
Per esempio, se α2 = 2poi α1 = -6. Sostituiamo questi valori nel sistema di equazioni sopra e otteniamo:
![]()
Risposta: così le linee s1 и s2 linearmente dipendente.